/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoboczny

Zadanie nr 2990127

Dodaj do ulubionych
Dodaj do rozwiązanych

Podstawa 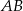AB trójkąta równobocznego 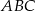ABC zawarta jest w prostej 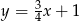y = 34x + 1 , a wierzchołek 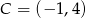C = (− 1,4) . Wyznacz współrzędne wierzchołków 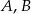A ,B tego trójkąta.

Rozwiązanie

Zaczynamy od rysunku

PIC

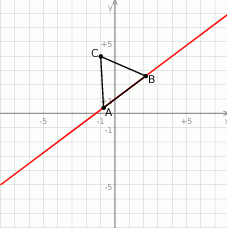
Ponieważ punkty 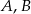A ,B leżą na prostej 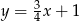y = 34x + 1 , więc wysokość (która jest prostopadła do podstawy) musi leżeć na prostej prostopadłej do prostej 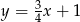y = 3x + 1 4 i przechodzącej przez punkt 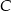C . Zatem długość wysokości będzie równa odległości punktu 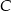C od prostej 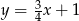3 y = 4x+ 1 . Liczymy

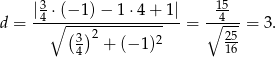
3 15 d = |4 ⋅∘(−-1)-−-1-⋅4+-1|= ∘-4---= 3. ( 3)2 2 25 4 + (− 1) 16

Wyznaczamy długość boku trójkąta

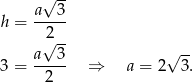
√ -- a---3 h = 2 √ -- √ -- 3 = a--3- ⇒ a = 2 3 . 2

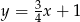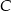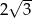Teraz musimy wyznaczyć punkty leżące na prostej 3 y = 4x+ 1 które są oddalone od punktu C o √ -- 2 3 . Dowolny punkt leżący na naszej prostej jest postaci

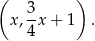
( ) 3- x,4 x + 1 .

Podstawiamy do równania i liczymy

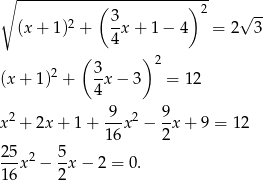
∘ -----------(------------)2- 2 3- √ -- (x + 1 ) + 4 x+ 1− 4 = 2 3 ( ) 2 2 3- (x + 1) + 4x − 3 = 12 x2 + 2x + 1 + -9-x2 − 9-x+ 9 = 12 1 6 2 25- 2 5- 16 x − 2x − 2 = 0.

Liczymy wyróżnik i pierwiastki

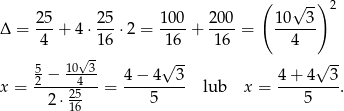
( ) 2 5 25 1 00 200 10√ 3- 2 Δ = ---+ 4⋅ ---⋅2 = ----+ ----= ------ 4 16 16 16 4 5 10√ 3 √ -- √ -- 2-−---4-- 4-−-4---3 4-+-4---3 x = 2 ⋅ 25 = 5 lub x = 5 . 16

Zatem punkty 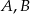A ,B mają współrzędne

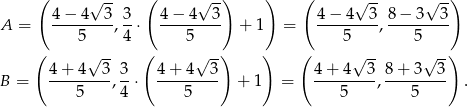
( ( ) ) ( ) √ -- √ -- √ -- √ -- A = 4-−-4--3-, 3-⋅ 4−--4--3- + 1 = 4-−-4--3-, 8-−-3-3- 5 4 5 5 5 ( √ -- ( √ -) ) ( √ -- √ -) 4+--4--3-3- 4+-4---3- 4-+-4--3- 8+--3--3- B = 5 ,4 ⋅ 5 + 1 = 5 , 5 .

 
Odpowiedź: ( √- √-) ( √- √-) A = 4−4-3, 8−-3-3- ,B = 4+-4-3, 8+-3-3 5 5 5 5

Wersja PDF