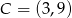Zadanie nr 3042704
Wierzchołki trójkąta równobocznego 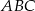 są punktami paraboli
są punktami paraboli 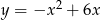 . Punkt
. Punkt 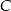 jest jej wierzchołkiem, a bok
jest jej wierzchołkiem, a bok 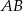 jest równoległy do osi
jest równoległy do osi 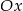 . Sporządź rysunek w układzie współrzędnych i wyznacz współrzędne wierzchołków tego trójkąta.
. Sporządź rysunek w układzie współrzędnych i wyznacz współrzędne wierzchołków tego trójkąta.
Rozwiązanie
Z równania paraboli
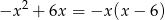
bez trudu odczytujemy jej punkty przecięcia z osią  , są to punkty
, są to punkty 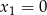 i
i 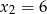 .
.
Wyznaczmy najpierw współrzędne punktu 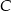 , czyli wierzchołka paraboli. W tym celu przedstawmy jej równanie w postaci kanonicznej:
, czyli wierzchołka paraboli. W tym celu przedstawmy jej równanie w postaci kanonicznej:
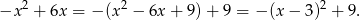
Otrzymujemy stąd 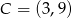 . W połączeniu z miejscami zerowymi pozwala nam to naszkicować schematyczny rysunek.
. W połączeniu z miejscami zerowymi pozwala nam to naszkicować schematyczny rysunek.
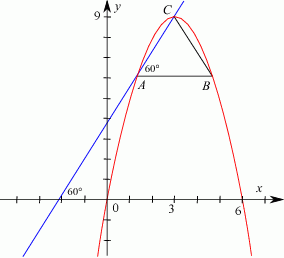
Wyznaczymy teraz równanie prostej 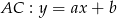 . Kąt jaki tworzy ona z osią
. Kąt jaki tworzy ona z osią  jest równy kątowi przy wierzchołku
jest równy kątowi przy wierzchołku 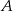 trójkąta
trójkąta 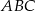 czyli wynosi
czyli wynosi 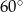 . Zatem
. Zatem 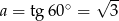 . Aby wyznaczyć
. Aby wyznaczyć  korzystamy z faktu, że zawiera ona punkt
korzystamy z faktu, że zawiera ona punkt 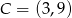 :
:
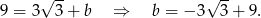
Możemy teraz wyznaczyć współrzędne punktu 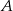 – jest to punkt przecięcia się paraboli i wyznaczonej prostej:
– jest to punkt przecięcia się paraboli i wyznaczonej prostej:
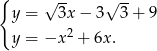
Odejmujemy od pierwszego równania drugie i otrzymujemy:
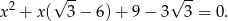
Równanie to ma dwa rozwiązania 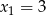 i
i 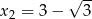 . Pierwsze z rozwiązań prowadzi do punktu
. Pierwsze z rozwiązań prowadzi do punktu 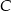 , a drugie daje nam
, a drugie daje nam 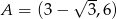 .
.
Ponieważ punkt 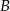 jest symetryczny do punktu
jest symetryczny do punktu 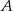 względem prostej
względem prostej 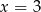 , to punkty te mają taką samą drugą współrzędną, a ich pierwsze współrzędne różnią się o
, to punkty te mają taką samą drugą współrzędną, a ich pierwsze współrzędne różnią się o
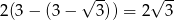
Otrzymujemy stąd 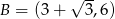 .
.
Odpowiedź: 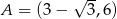 ,
, 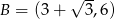 ,
,