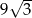/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoboczny

Zadanie nr 4695717

Dodaj do ulubionych
Dodaj do rozwiązanych

W trójkącie równobocznym 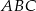ABC dane są wierzchołek 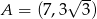√ -- A = (7,3 3) i środek okręgu wpisanego 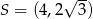√ -- S = (4,2 3) . Oblicz pole trójkąta ABC .

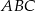Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

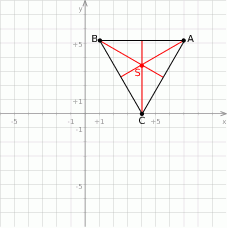
Obliczmy długość odcinka 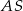AS .

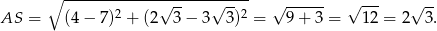
∘ -------------√------√----- √ ------ √ --- √ -- AS = (4− 7)2 + (2 3− 3 3)2 = 9 + 3 = 1 2 = 2 3.

Wiemy, że środek trójkąta równobocznego dzieli jego wysokości w stosunku 2:1, więc łatwo możemy wyliczyć długość wysokości 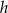h tego trójkąta.

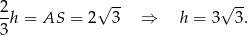
2- √ -- √ -- 3 h = AS = 2 3 ⇒ h = 3 3.

To pozwala wyliczyć długość boku trójkąta

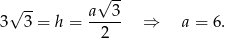
√ -- √ -- a--3- 3 3 = h = 2 ⇒ a = 6.

Zatem pole trójkąta jest równe

√ -- a2 3 √ -- P = --4---= 9 3 .

 
Odpowiedź: √ -- 9 3

Wersja PDF