Zadanie nr 7303723
Napisz równanie okręgu stycznego do osi 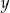 w punkcie
w punkcie 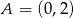 i przechodzącego przez punkt
i przechodzącego przez punkt 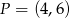 . Wyznacz na okręgu takie punkty
. Wyznacz na okręgu takie punkty 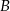 i
i 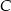 , aby trójkąt
, aby trójkąt 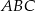 był równoboczny.
był równoboczny.
Rozwiązanie
Zacznijmy od szkicowego rysunku.
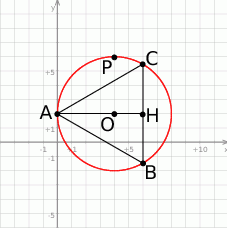
Informacja o tym, że szukany okrąg jest styczny do osi 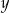 w punkcie
w punkcie 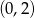 oznacza, że jego środek leży na prostej
oznacza, że jego środek leży na prostej 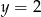 . Aby ten środek wyznaczyć musimy na tej prostej znaleźć punkt
. Aby ten środek wyznaczyć musimy na tej prostej znaleźć punkt 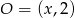 , który jest równoodległy od punktów
, który jest równoodległy od punktów 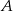 i
i 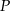 . Mamy więc równanie
. Mamy więc równanie
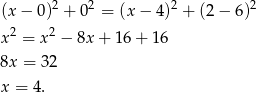
A więc środkiem szukanego okręgu jest punkt 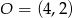 , a jego promień jest równy 4. Możemy napisać równanie okręgu.
, a jego promień jest równy 4. Możemy napisać równanie okręgu.
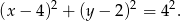
Ponieważ wiemy, że prosta 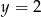 zawiera wysokość
zawiera wysokość 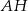 szukanego trójkąta równobocznego, oraz
szukanego trójkąta równobocznego, oraz 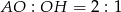 , więc spodek wysokości
, więc spodek wysokości 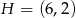 . Zatem prosta
. Zatem prosta 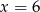 zawiera bok
zawiera bok 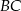 . Pozostało znaleźć jej punkty wspólne z naszym okręgiem.
. Pozostało znaleźć jej punkty wspólne z naszym okręgiem.
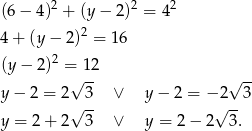
Odpowiedź: 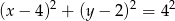 ,
, 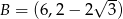 ,
,