/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoboczny

Zadanie nr 9419297

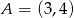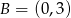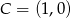Punkty A = (3,4) , B = (0,3 ) i C = (1,0) należą do okręgu. Oblicz pole trójkąta równobocznego opisanego na tym okręgu.

Wersja PDF

Rozwiązanie

Jeżeli zaznaczymy podane punkty w układzie współrzędnych to wydaje się, że trójkąt 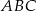ABC jest prostokątny - sprawdźmy czy tak jest (z twierdzenia odwrotnego do twierdzenia Pitagorasa).

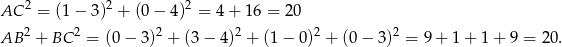
AC 2 = (1 − 3)2 + (0 − 4)2 = 4 + 16 = 20 2 2 2 2 2 2 AB + BC = (0 − 3) + (3− 4) + (1− 0) + (0 − 3 ) = 9+ 1+ 1+ 9 = 20.

Zatem istotnie kąt przy wierzchołku 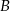B jest prosty i okrąg opisany na trójkącie 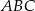ABC , to okrąg o środku w połowie przeciwprostokątnej i promieniu

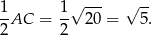
1 1√ --- √ -- -AC = -- 20 = 5. 2 2

Ponieważ promień okręgu wpisanego w trójkąt równoboczny o boku a jest równy

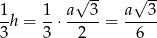
√ -- √ -- 1-h = 1-⋅ a--3 = a---3 3 3 2 6

to mamy równanie

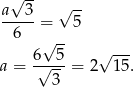
√ -- √ -- a--3-= 5 6 √ -- 6 5 √ --- a = -√--- = 2 15 . 3

Zatem pole trójkąta wynosi

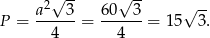
2√ -- √ -- √ -- P = a---3-= 6-0--3 = 15 3. 4 4

 
Odpowiedź: √ -- 15 3

Wersja PDF