/Szkoła średnia/Geometria/Geometria analityczna/Trójkąt/Równoboczny

Zadanie nr 9592553

Dany jest okrąg 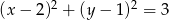2 2 (x− 2) + (y− 1) = 3 . Oblicz pole trójkąta równobocznego wpisanego w ten okrąg.

Wersja PDF

Rozwiązanie

Jedyna informacja dotycząca podanego okręgu, która jest istotna to jego promień 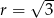√ -- r = 3 . Położenie tego okręgu w układzie współrzędnych nie ma żadnego znaczenia.

Wykonajmy rysunek.

PIC

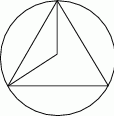
Jeżeli bok tego trójkąta równobocznego oznaczymy przez a , to ze wzoru na wysokość w trójkącie równobocznym mamy

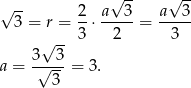
√ -- √ -- √ -- 2- a--3- a--3- 3 = r = 3 ⋅ 2 = 3 √ -- a = 3√-3-= 3. 3

Ze wzoru na pole trójkąta równobocznego mamy

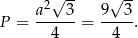
√ -- √ -- a-2--3 9--3- P = 4 = 4 .

 
Odpowiedź: √ - 9--3 4

Wersja PDF