Zadanie nr 2060973
Obwód trapezu równoramiennego wynosi 32 cm. Wysokość poprowadzona z wierzchołka kąta rozwartego dzieli podstawę na dwa odcinki o długościach 3 cm i 11 cm. Oblicz pole trapezu.
Rozwiązanie
Zaczynamy od rysunku.
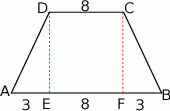
Ponieważ trapez jest równoramienny, jeżeli poprowadzimy wysokości z wierzchołków  i
i 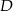 to
to 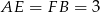 . Stąd
. Stąd 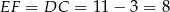 . Za podanego obwodu mamy
. Za podanego obwodu mamy
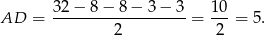
Liczymy teraz wysokość trapezu z twierdzenia Pitagorasa w trójkącie 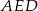 .
.
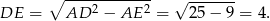
Zatem pole trapezu jest równe
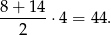
Odpowiedź: