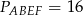Zadanie nr 3712905
W trapezie 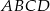 o podstawach
o podstawach 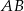 i
i 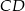 dane są długości przekątnych
dane są długości przekątnych 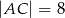 i
i 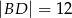 oraz pola
oraz pola 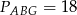 i
i 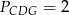 . Punkty
. Punkty 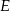 i
i 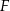 są środkami odpowiednio przekątnych
są środkami odpowiednio przekątnych 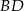 i
i 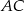 .
.
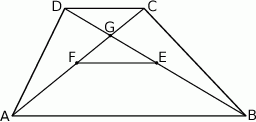
Oblicz pole trapezu 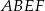 .
.
Rozwiązanie
Zauważmy najpierw, że trójkąty 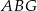 i
i 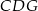 są podobne (bo mają równe kąty) oraz znamy ich skalę podobieństwa
są podobne (bo mają równe kąty) oraz znamy ich skalę podobieństwa
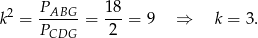
Zatem
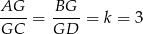
oraz
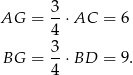
Stąd
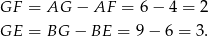
To oznacza, że trójkąty 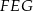 i
i 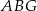 są podobne w skali
są podobne w skali 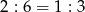 (bo mają wspólny kąt i proporcjonalne boki przylegające do tego kąta). Zatem
(bo mają wspólny kąt i proporcjonalne boki przylegające do tego kąta). Zatem
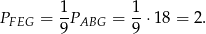
Stąd
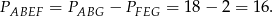
Odpowiedź: