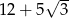Zadanie nr 4899344
Wiedząc, że 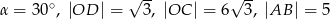 oraz
oraz 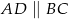 , oblicz pole i obwód trapezu
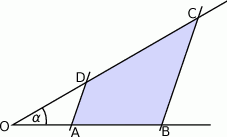
, oblicz pole i obwód trapezu  przedstawionego na rysunku.
przedstawionego na rysunku.
Rozwiązanie
Podpiszmy podane długości odcinków.
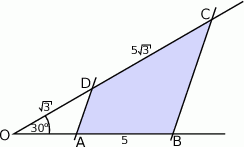
Korzystając z twierdzenia Talesa, łatwo obliczyć długość odcinka 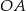 .
.
W takim razie możemy policzyć pola trójkątów  i
i 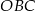 (ze wzoru z sinusem). Pole trapezu to różnica pól tych trójkątów
(ze wzoru z sinusem). Pole trapezu to różnica pól tych trójkątów
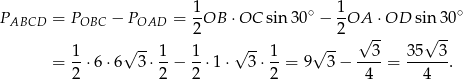
Do wyliczenia obwodu brakuje nam jeszcze długości odcinków 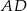 i
i 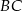 . Długość pierwszego z nich możemy wyliczyć z twierdzenia cosinusów w trójkącie
. Długość pierwszego z nich możemy wyliczyć z twierdzenia cosinusów w trójkącie 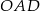 .
.
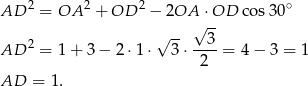
Do wyliczenia długości odcinka 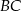 wystarczy nam już twierdzenie Talesa.
wystarczy nam już twierdzenie Talesa.
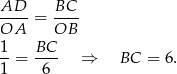
Zatem obwód trapezu jest równy
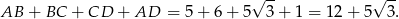
Odpowiedź: Pole: 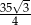 , obwód:
, obwód: