/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez

Zadanie nr 5801025

Dodaj do ulubionych
Dodaj do rozwiązanych

Promień koła wpisanego w trapez prostokątny jest równy r , kąt ostry trapezu równy jest α . Oblicz pole i obwód trapezu.

Rozwiązanie

Rozpoczynamy od szkicowego rysunku.

PIC

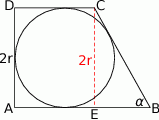
W trójkącie 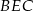BEC mamy

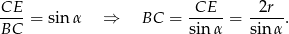
CE--= sinα ⇒ BC = -CE-- = --2r-. BC sinα sin α

Wiemy ponadto, że w czworokącie opisanym na okręgu sumy długości przeciwległych boków są równe, zatem obwód trapezu jest równy

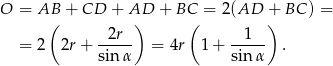
O = AB( + CD + A)D + BC( = 2 (AD +) BC ) = 2r 1 = 2 2r + ----- = 4r 1+ ----- . sin α sin α

Pozostało obliczyć pole

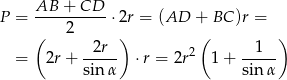
AB + CD P = ----------⋅2r = (AD + BC )r = ( 2 ) ( ) = 2r + --2r- ⋅ r = 2r2 1+ --1-- sin α sinα

 
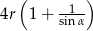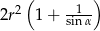Odpowiedź: Obwód: ( ) 4r 1+ -1-- sinα , pole: ( ) 2r2 1 + --1- sin α .

Wersja PDF