Zadanie nr 6543735
Ramiona trapezu mają długości 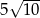 i 20. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
i 20. Przekątne w tym trapezie są prostopadłe, a punkt ich przecięcia dzieli je w stosunku 2:3. Oblicz pole tego trapezu.
Rozwiązanie
Szkicujemy opisaną sytuację.
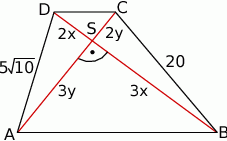
Wiemy, że przekątne trapezu dzielą się w stosunku 2:3, więc możemy oznaczyć długości odcinków, na które się dzielą przez 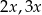 i
i 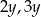 jak na rysunku powyżej. Stosujemy teraz twierdzenie Pitagorasa w trójkątach prostokątnych
jak na rysunku powyżej. Stosujemy teraz twierdzenie Pitagorasa w trójkątach prostokątnych 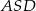 i
i 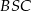 .
.
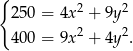
Rozwiązujemy teraz powyższy układ równań – mnożymy pierwsze równanie przez 9, a drugie przez 4 i odejmujemy tak otrzymane równania stronami
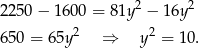
Stąd
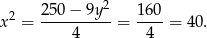
Pole trapezu  obliczamy jako sumę 4 trójkątów prostokątnych.
obliczamy jako sumę 4 trójkątów prostokątnych.
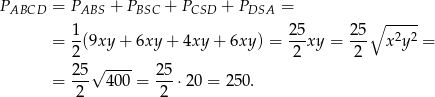
Odpowiedź: 250

