/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez

Zadanie nr 7682987

Dodaj do ulubionych
Dodaj do rozwiązanych

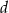W półkole o promieniu r wpisano trapez równoramienny o przekątnej długości d . Oblicz długość krótszej podstawy trapezu.

PIC

Rozwiązanie

Sposób I

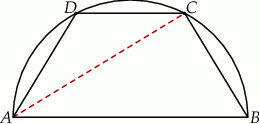
Zauważmy najpierw, że trójkąt 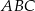ABC jest prostokątny – tak jest, bo kąt 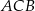ACB jest oparty na średnicy.

PIC

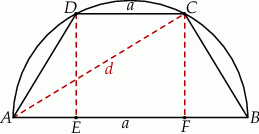
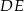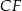Dorysujmy wysokości DE i CF trapezu. Otrzymaliśmy w ten sposób jeszcze jeden trójkąt prostokątny 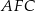AF C , który jest podobny do trójkąta 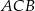ACB (bo oba są prostokątne i mają wspólny kąt przy wierzchołku 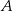A ). Z tego podobieństwa mamy

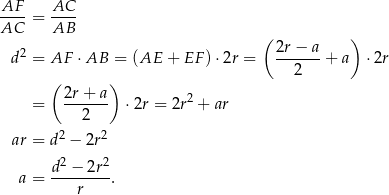
AF-- AC-- AC = AB ( 2r − a ) d2 = AF ⋅AB = (AE + EF) ⋅2r = ------ + a ⋅2r ( ) 2 2r + a 2 = ------ ⋅2r = 2r + ar 2 ar = d2 − 2r2 2 2 a = d--−-2r- . r

Sposób II

Tym razem skorzystamy z faktu, że wysokość w trójkącie prostokątnym jest średnią geometryczną długości odcinków, na jakie dzieli przeciwprostokątną. Na naszym obrazku oznacza to, że

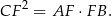
CF 2 = AF ⋅F B.

Teraz korzystamy z twierdzenia Pitagorasa w trójkącie 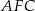AF C .

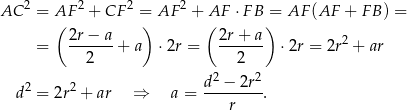
AC 2 = AF 2 + CF 2 = AF 2 + AF ⋅F B = AF (AF + FB ) = ( ) ( ) = 2r-−-a + a ⋅2r = 2r-+-a ⋅ 2r = 2r2 + ar 2 2 d2 − 2r2 d2 = 2r2 + ar ⇒ a = --------. r

 
Odpowiedź: d2−2r2 ---r--

Wersja PDF