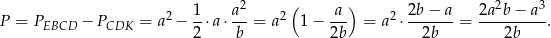/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez

Zadanie nr 7968221

Dodaj do ulubionych
Dodaj do rozwiązanych

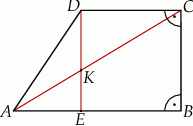
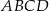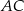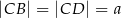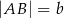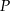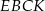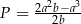W trapezie prostokątnym ABCD (rysunek) punkt K jest punktem przecięcia wysokości DE i przekątnej AC tego trapezu. Wiedząc, że |CB | = |CD | = a i |AB | = b wykaż, że pole P czworokąta EBCK jest równe P = 2a2b−a-3 2b .

PIC

Rozwiązanie

Zauważmy najpierw, że 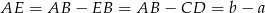AE = AB − EB = AB − CD = b− a .

Sposób I

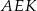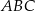Trójkąty AEK i ABC sa podobne, więc

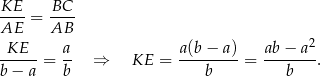
KE-- BC-- AE = AB 2 -KE---= a- ⇒ KE = a(b−--a)-= ab-−-a--. b − a b b b

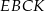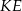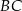Czworokąt EBCK jest trapezem prostokątnym o podstawach KE i BC oraz wysokości 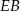EB . Jego pole jest więc równe

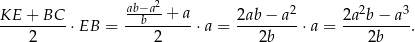
2 KE + BC ab−ba-+ a 2ab − a2 2a2b− a3 ----------⋅EB = ---------⋅ a = ---------⋅a = ---------. 2 2 2b 2b

Sposób II

Tak jak poprzednio obliczamy: 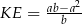KE = ab−a2 b . Pole czworokąta 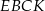EBCK obliczamy jako różnicę pól trójkątów 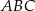ABC i AEK .

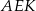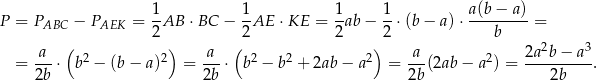
1 1 1 1 a (b− a ) P = PABC − PAEK = -AB ⋅BC − --AE ⋅ KE = -ab − -⋅ (b− a)⋅---------= 2 2 2 2 b a-- ( 2 2) a-- ( 2 2 2) -a- 2 2a2b-−-a3- = 2b ⋅ b − (b − a) = 2b ⋅ b − b + 2ab − a = 2b (2ab− a ) = 2b .

Sposób III

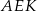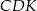Trójkąty AEK i CDK mają równe kąty, więc są podobne. Mamy zatem

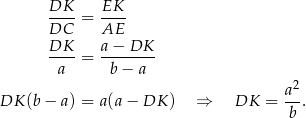
DK-- EK-- DC = AE DK a− DK ----= -------- a b − a a2- DK (b − a) = a(a− DK ) ⇒ DK = b .

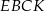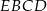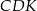Pole czworokąta EBCK obliczamy jako różnicę pól kwadratu EBCD i trójkąta prostokątnego CDK .

2 1 a2 2 ( a ) 2 2b − a 2a2b − a3 P = PEBCD − PCDK = a − --⋅a ⋅---= a 1 − --- = a ⋅-------= ---------. 2 b 2b 2b 2b
Wersja PDF