/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez

Zadanie nr 8327579

Dodaj do ulubionych
Dodaj do rozwiązanych

Ramiona trapezu prostokątnego mają długości 6 i 10. Odcinek łączący środki ramion ma długość 10. Oblicz długości podstaw trapezu.

Rozwiązanie

Zaczynamy od rysunku.

PIC

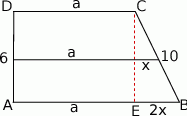
Jeżeli oznaczymy długość krótszej podstawy przez a oraz kawałek odcinka łączącego środki ramion trapezu odciętego przez wysokość przez x (jak na rysunku), to mamy

x = 10 − a.

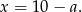
Ponadto z twierdzenia Talesa,

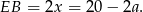
EB = 2x = 20 − 2a.

Napiszmy teraz twierdzenie Pitagorasa w trójkącie 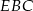EBC .

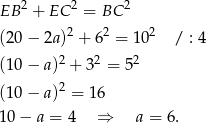
EB 2 + EC 2 = BC 2 2 2 2 (20 − 2a) + 6 = 10 / : 4 (10 − a)2 + 32 = 52 (10 − a)2 = 16 10 − a = 4 ⇒ a = 6.

Zatem podstawy mają długości 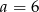a = 6 i

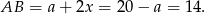
AB = a + 2x = 20 − a = 14.

 
Odpowiedź: 6 i 14

Wersja PDF