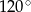/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez

Zadanie nr 8339038

Dodaj do ulubionych
Dodaj do rozwiązanych

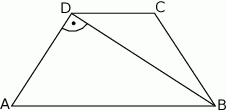
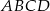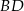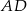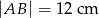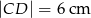W trapezie równoramiennym ABCD przekątna BD jest prostopadła do ramienia AD (zobacz rysunek). Podstawy trapezu mają długość: |AB | = 12 cm i |CD | = 6 cm . Oblicz pole oraz miary kątów trapezu.

PIC

Rozwiązanie

Dorysujmy wysokości trapezu

PIC

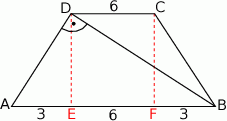
Zauważmy, że

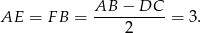
AE = FB = AB--−-DC--= 3. 2

Ponadto trójkąty AED i DEB są podobne (bo oba są podobne do trójkąta ADB ). Zatem

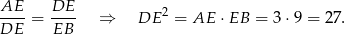
AE-- = DE-- ⇒ DE 2 = AE ⋅ EB = 3⋅ 9 = 27. DE EB

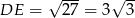Stąd √ --- √ -- DE = 2 7 = 3 3 i pole trapezu jest równe

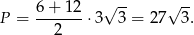
6+ 12 √ -- √ -- P = -------⋅3 3 = 27 3. 2

Aby obliczyć miary kątów zauważmy, że

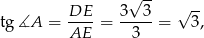
DE 3 √ 3- √ -- tg∡A = ---- = ----- = 3, AE 3

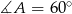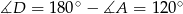czyli ∘ ∡A = 60 . Zatem ∘ ∘ ∡D = 1 80 − ∡A = 12 0 .  
Odpowiedź: 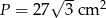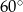√ -- P = 27 3 cm 2 , 60∘ i 1 20∘

Wersja PDF