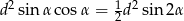/Szkoła średnia/Geometria/Planimetria/Czworokąt/Trapez

Zadanie nr 9169248

Dodaj do ulubionych
Dodaj do rozwiązanych

W trapezie równoramiennym przekątna ma długość 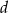d i tworzy z dłuższą podstawą kąt o mierze α . Oblicz pole tego trapezu.

Rozwiązanie

Narysujmy sobie opisaną sytuację i oznaczmy podstawy trapezu przez a i b .

PIC

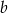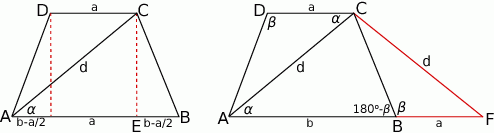
Sposób I

Ponieważ trapez jest równoramienny mamy

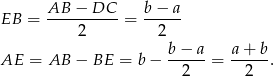
AB − DC b− a EB = ----------= ------ 2 2 AE = AB − BE = b − b-−-a-= a+--b. 2 2

Jeżeli popatrzymy na trójkąt prostokątny 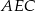AEC to mamy

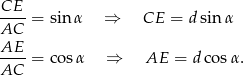
CE ---- = sin α ⇒ CE = d sin α AC AE-- AC = cos α ⇒ AE = dco sα.

Ponieważ zauważyliśmy, że 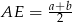AE = a+2b- , więc pole jest równe

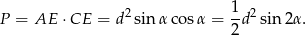
P = AE ⋅ CE = d2sin αco sα = 1d2 sin 2α. 2

Sposób II

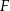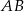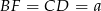Niech F będzie takim punktem na przedłużeniu podstawy AB , że BF = CD = a . Ponieważ

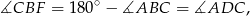
∘ ∡CBF = 18 0 − ∡ABC = ∡ADC ,

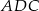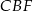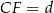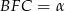trójkąty ADC i CBF są przystające. Zatem CF = d i BF C = α . Patrzymy teraz na trójkąt 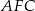AF C . Jest to trójkąt równoramienny i jego pole jest równe polu trapezu, zatem ze wzoru z sinusem na pole trójkąta mamy

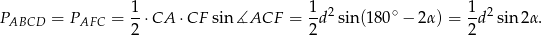
P = P = 1-⋅CA ⋅CF sin∡ACF = 1-d2sin(180∘ − 2α) = 1d2 sin 2α . ABCD AFC 2 2 2

 
Odpowiedź: 2 1 2 d sin α cosα = 2d sin 2α

Wersja PDF