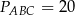Zadanie nr 1985173
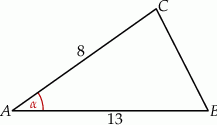
W trójkącie 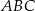 dane są długości boków
dane są długości boków 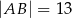 i
i 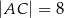 oraz
oraz 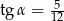 , gdzie
, gdzie 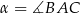 . Oblicz pole trójkąta
. Oblicz pole trójkąta 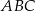 .
.
Rozwiązanie
Obliczmy najpierw 
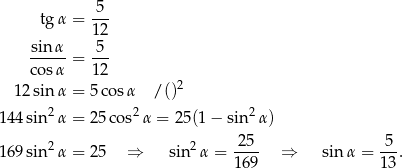
Pole trójkąta 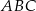 jest więc równe
jest więc równe
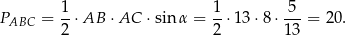
Odpowiedź: 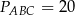
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie 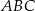 dane są długości boków
dane są długości boków 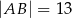 i
i 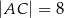 oraz
oraz 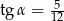 , gdzie
, gdzie 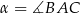 . Oblicz pole trójkąta
. Oblicz pole trójkąta 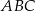 .
.

Obliczmy najpierw 
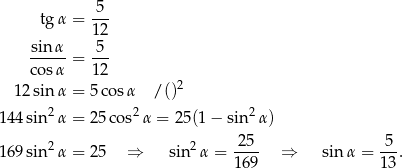
Pole trójkąta 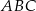 jest więc równe
jest więc równe
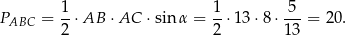
Odpowiedź: