/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Pole

Zadanie nr 2009420

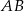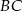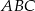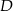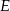Na bokach AB i BC trójkąta ABC wybrano punkty D i E w ten sposób, że odcinek 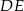DE jest styczny do okręgu wpisanego w trójkąt 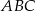ABC oraz trójkąt 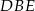DBE jest równoboczny. Obwód trójkąta 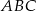ABC jest równy 20, a długość boku 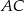AC jest równa 7. Oblicz pole trójkąta DBE .

PIC

Wersja PDF

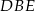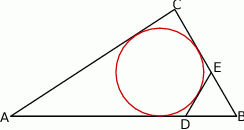
Rozwiązanie

Niech 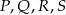P,Q ,R ,S będą punktami styczności okręgu wpisanego w trójkąt z jego bokami oraz odcinkiem DE .

PIC

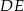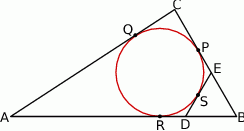
Jeżeli oznaczymy 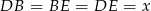DB = BE = DE = x , to

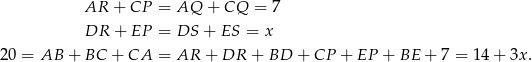
AR + CP = AQ + CQ = 7 DR + EP = DS + ES = x 20 = AB + BC + CA = AR + DR + BD + CP + EP + BE + 7 = 14 + 3x .

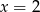Stąd x = 2 i pole trójkąta 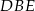DBE jest równe

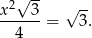
√ -- x2 3 √ -- --4---= 3.

 
Odpowiedź: √ -- 3

Wersja PDF