Zadanie nr 2656717
Punkt 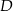 leży na boku
leży na boku 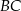 trójkąta
trójkąta 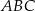 oraz
oraz 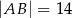 ,
, 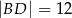 ,
, 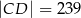 i
i 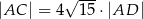 . Oblicz pole trójkąta
. Oblicz pole trójkąta 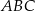 .
.
Rozwiązanie
Narysujmy opisaną sytuację.
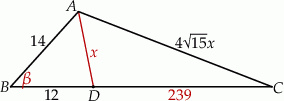
Piszemy twierdzenia cosinusów w trójkątach 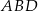 i
i 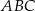 .
.
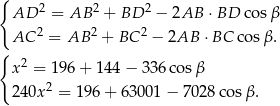
Odejmujemy teraz od drugiego równania pierwsze pomnożone przez 240.
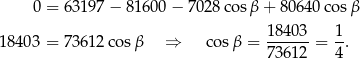
Podstawiamy tę wartość do pierwszego równania
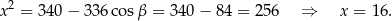
Pole trójkąta 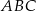 obliczymy na dwa sposoby.
obliczymy na dwa sposoby.
Sposób I
Pole obliczymy ze wzoru na pole z sinusem. Zauważmy najpierw, że
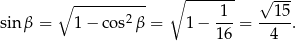
Pole trójkąta jest więc równe
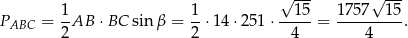
Sposób II
Pole możemy też obliczyć ze wzoru Herona
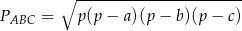
gdzie
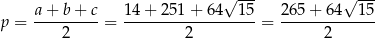
jest połową obwodu trójkąta. Mamy zatem
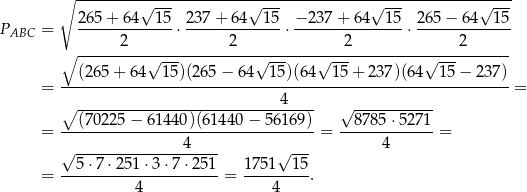
Odpowiedź: