/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Pole

Zadanie nr 3638718

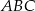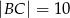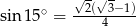Oblicz pole trójkąta ABC przedstawionego na rysunku, jeśli wiadomo, że |BC | = 10 oraz √ - √- sin 15∘ = --2(-3−1) 4 .

PIC

Wersja PDF

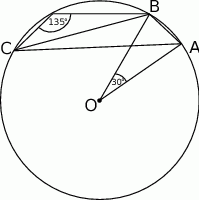
Rozwiązanie

Zaczynamy od dopisania na rysunku tego, co tylko się da.

PIC

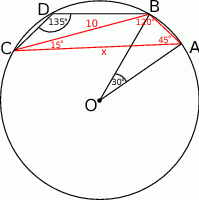
Ponieważ kąt wpisany 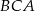BCA jest oparty na tym samym łuku co kąt środkowy 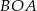BOA , to

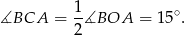
∡BCA = 1-∡BOA = 15∘. 2

Ponadto czworokąt 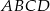ABCD jest wpisany w okrąg, czyli

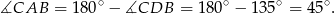
∡CAB = 180∘ − ∡CDB = 180∘ − 13 5∘ = 45∘.

Zatem

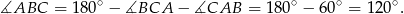
∡ABC = 18 0∘ − ∡BCA − ∡CAB = 180∘ − 60∘ = 1 20∘.

Widać teraz, że łatwo możemy wyliczyć długość boku 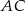AC – stosujemy twierdzenie sinusów

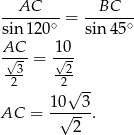
--AC---- = --BC--- sin12 0∘ sin 45∘ AC 10 √-3-= √-2 -2- -2- 10√ 3- AC = -√---. 2

Pozostało policzyć pole (ze wzoru z sinusem).

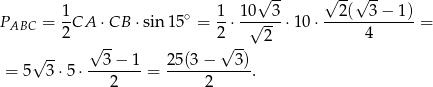
√ -- √ --√ -- 1 ∘ 1 10 3 2( 3− 1) PABC = -CA ⋅CB ⋅sin15 = --⋅-√----⋅1 0⋅ -------------= 2 √ -- 2√ -- 2 4 √ -- --3-−-1- 25(3-−---3-) = 5 3⋅5 ⋅ 2 = 2 .

 
Odpowiedź: √ - 25(3−2--3)

Wersja PDF