Zadanie nr 4686652
Dany jest trójkąt 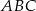 , w którym
, w którym 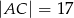 i
i 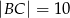 . Na boku
. Na boku 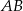 leży punkt
leży punkt 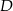 taki, że
taki, że 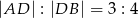 oraz
oraz 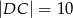 . Oblicz pole trójkąta
. Oblicz pole trójkąta 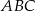 .
.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
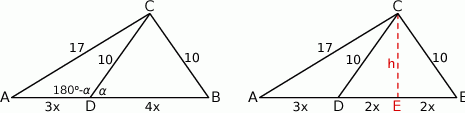
Sposób I
Oznaczmy 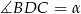 . Wtedy oczywiście
. Wtedy oczywiście 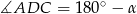 . Piszemy teraz twierdzenia cosinusów w trójkątach
. Piszemy teraz twierdzenia cosinusów w trójkątach 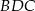 i
i 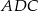 .
.
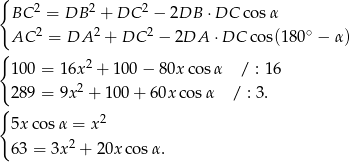
Podstawiamy teraz 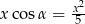 z pierwszego równania do drugiego.
z pierwszego równania do drugiego.
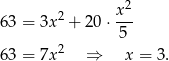
W takim razie 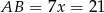 i pole trójkąta
i pole trójkąta 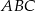 możemy obliczyć ze wzoru Herona.
możemy obliczyć ze wzoru Herona.
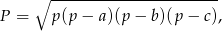
gdzie 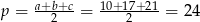 jest połową obwodu. Mamy zatem
jest połową obwodu. Mamy zatem
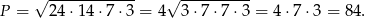
Sposób II
Tym razem obejdziemy się bez twierdzenia cosinusów. Dorysujmy wysokość 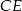 opuszczoną z wierzchołka
opuszczoną z wierzchołka 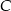 . Zauważmy, że trójkąt
. Zauważmy, że trójkąt 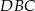 jest równoramienny, więc
jest równoramienny, więc 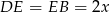 . Piszemy teraz twierdzenie Pitagorasa w trójkątach
. Piszemy teraz twierdzenie Pitagorasa w trójkątach 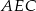 i
i 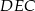 .
.
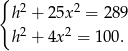
Odejmujemy teraz od pierwszego równania drugie i mamy

Z drugiego równania mamy więc
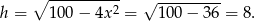
W takim razie pole trójkąta 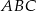 jest równe
jest równe
Odpowiedź: 84

