/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Pole

Zadanie nr 4839875

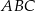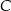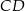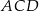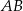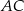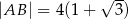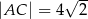W trójkącie rozwartokątnym ABC o kącie rozwartym przy wierzchołku C poprowadzono wysokość CD i otrzymano równoramienny trójkąt ACD . Długości boków AB i AC są odpowiednio równe √ -- |AB | = 4(1+ 3) i √ -- |AC | = 4 2 . Oblicz pole powierzchni koła opisanego na trójkącie ABC .

Wersja PDF

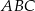Rozwiązanie

Szkicujemy opisaną sytuację.

PIC

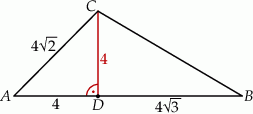
Wiemy, że trójkąt prostokątny 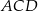ACD jest równoramienny, więc jest to połówka kwadratu i

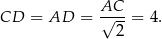
CD = AD = A√C--= 4 . 2

Stąd

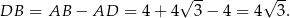
√ -- √ -- DB = AB − AD = 4+ 4 3− 4 = 4 3.

Stosujemy teraz twierdzenie Pitagorasa w trójkącie prostokątnym 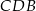CDB .

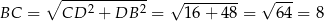
∘ ------------ √ -------- √ --- BC = CD 2 + DB 2 = 16 + 48 = 64 = 8

(mogliśmy też zauważyć, że trójkąt 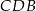CDB to połówka trójkąta równobocznego).

Zastanówmy się do czego zmierzamy – promień 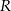R koła opisanego na trójkącie 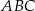ABC możemy z twierdzenia sinusów

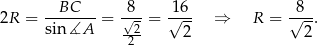
BC 8 16 8 2R = ------- = √--= √--- ⇒ R = √--. sin ∡A -22 2 2

Jeżeli ktoś nie chce korzystać z twierdzenia sinusów, to do tego samego wniosku możemy dojść porównując dwa wzory na pole

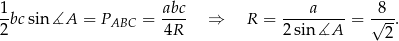
1bcsin ∡A = PABC = abc- ⇒ R = ---a-----= √8-. 2 4R 2sin∡A 2

Pole koła opisanego na trójkącie 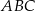ABC jest więc równe

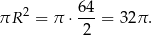
πR 2 = π ⋅ 64-= 32π . 2

 
Odpowiedź: 32π

Wersja PDF