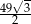Zadanie nr 5594230
W trójkącie 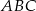 dane są:
dane są: 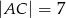 ,
, 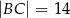 i
i 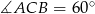 . Oblicz pole trójkąta
. Oblicz pole trójkąta 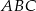 .
.
Rozwiązanie
Szkicujemy opisany trójkąt.
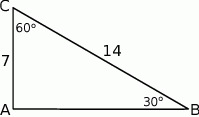
Z rysunku powinno być jasne, że trójkąt 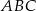 to połówka trójkąta równobocznego o boku długości
to połówka trójkąta równobocznego o boku długości 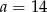 (jest przystający do połówki trójkąta równobocznego zgodnie z cechą
(jest przystający do połówki trójkąta równobocznego zgodnie z cechą 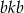 ). W szczególności jest to trójkąt prostokątny:
). W szczególności jest to trójkąt prostokątny: 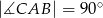 .
.
Sposób I
Jego pole jest więc równe
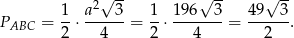
Sposób II
Korzystamy ze wzoru na pole z sinusem.
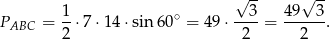
Odpowiedź: