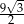Zadanie nr 5829617
W trójkącie 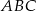 dane są
dane są 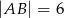 ,
, 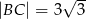 oraz
oraz 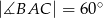 . Oblicz pole trójkąta
. Oblicz pole trójkąta 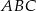 .
.
Rozwiązanie
Zacznijmy od rysunku.
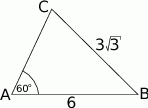
Na początku wyliczmy z twierdzenia cosinusów długość boku 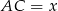 .
.
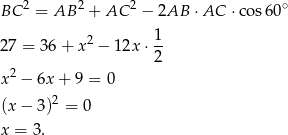
Stąd
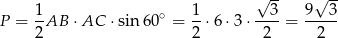
Odpowiedź: 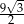
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
W trójkącie  dane są
dane są 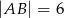 ,
, 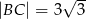 oraz
oraz 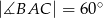 . Oblicz pole trójkąta
. Oblicz pole trójkąta 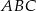 .
.
Zacznijmy od rysunku.

Na początku wyliczmy z twierdzenia cosinusów długość boku 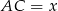 .
.
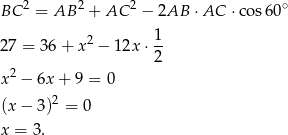
Stąd
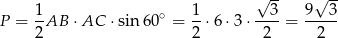
Odpowiedź: