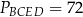Zadanie nr 6159565
W trójkącie 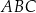 dane są długości boków
dane są długości boków 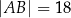 i
i 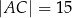 oraz
oraz 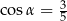 , gdzie
, gdzie 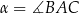 . Na bokach
. Na bokach 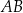 i
i 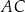 tego trójkąta obrano punkty odpowiednio
tego trójkąta obrano punkty odpowiednio 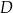 i
i 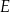 takie, że
takie, że 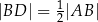 i
i 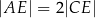 (zobacz rysunek).
(zobacz rysunek).

Oblicz pole
-
trójkąta
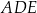 .
. -
czworokąta
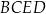 .
.
Rozwiązanie
Korzystając z jedynki trygonometrycznej obliczamy  .
.
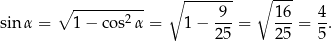
-
Zauważmy najpierw, że
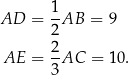
Obliczamy teraz pole trójkąta
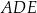 – korzystamy ze wzoru na pole z sinusem.
– korzystamy ze wzoru na pole z sinusem. 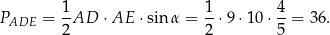
Odpowiedź: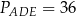
-
Obliczamy najpierw pole trójkąta
 .
. 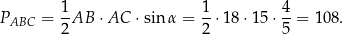
Pole czworokąta
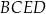 jest więc równe
jest więc równe 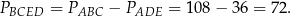
Odpowiedź: