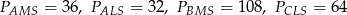Zadanie nr 6399094
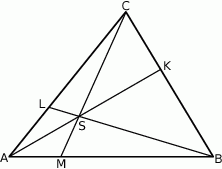
Punkty 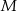 i
i 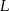 leżą odpowiednio na bokach
leżą odpowiednio na bokach 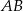 i
i 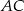 trójkąta
trójkąta 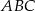 , przy czym zachodzą równości
, przy czym zachodzą równości 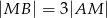 oraz
oraz 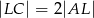 . Punkt
. Punkt 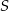 jest punktem przecięcia odcinków
jest punktem przecięcia odcinków 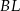 i
i 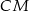 . Punkt
. Punkt 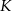 jest punktem przecięcia półprostej
jest punktem przecięcia półprostej 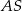 z odcinkiem
z odcinkiem 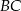 (zobacz rysunek).
(zobacz rysunek).
Pole trójkąta 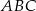 jest równe 528. Oblicz pola trójkątów:
jest równe 528. Oblicz pola trójkątów: 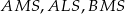 i
i 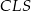 .
.
Rozwiązanie
Sposób I
Zauważmy, że trójkąty 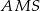 i
i 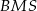 mają wspólną wysokość opuszczoną na prostą
mają wspólną wysokość opuszczoną na prostą  , a stosunek ich podstaw jest równy
, a stosunek ich podstaw jest równy 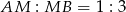 .
.
W takim razie taki sam jest stosunek ich pól, więc możemy je oznaczyć przez 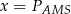 i
i 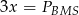 . Analogicznie uzasadniamy, że stosunek pól trójkątów
. Analogicznie uzasadniamy, że stosunek pól trójkątów 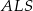 i
i 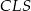 jest równy
jest równy 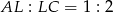 , więc możemy je oznaczyć przez
, więc możemy je oznaczyć przez 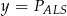 i
i 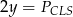 .
.
Aby obliczyć  i
i 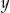 potrzebujemy dwa równania wiążące ze sobą te niewiadome. Gdy popatrzymy na rysunek łatwo się domyślić skąd wziąć te równania – wystarczy napisać równania wyrażające pola trójkątów
potrzebujemy dwa równania wiążące ze sobą te niewiadome. Gdy popatrzymy na rysunek łatwo się domyślić skąd wziąć te równania – wystarczy napisać równania wyrażające pola trójkątów 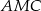 i
i 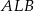 . Trójkąty
. Trójkąty 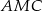 i
i 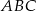 mają wspólną wysokość opuszczoną na prostą
mają wspólną wysokość opuszczoną na prostą 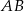 , więc stosunek ich pól jest równy stosunkowi ich podstaw. Zatem
, więc stosunek ich pól jest równy stosunkowi ich podstaw. Zatem
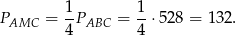
Analogicznie
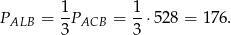
Pozostało rozwiązać układ równań
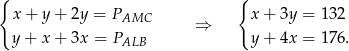
Odejmujemy od pierwszego równania drugie pomnożone przez 3 (żeby skrócić 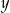 ) i mamy
) i mamy
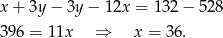
Stąd 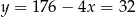 . Mamy zatem
. Mamy zatem
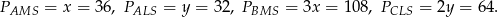
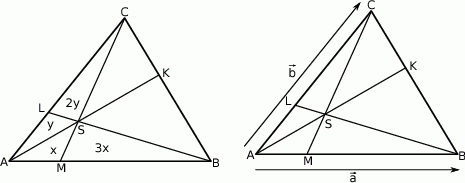
Sposób II
Tym razem użyjemy rachunku wektorowego, aby obliczyć w jakim stosunku dzielą się odcinki 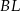 i
i 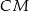 . Oznaczmy
. Oznaczmy 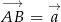 ,
, 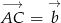 ,
, 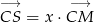 ,
, 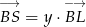 . Patrząc na trójkąty
. Patrząc na trójkąty 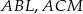 mamy
mamy
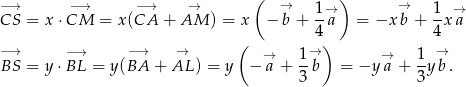
Teraz patrzymy na trójkąt 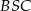 .
.
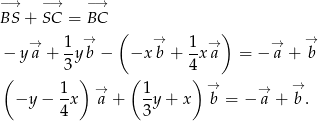
Porównujemy teraz współczynniki przy 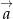 i
i 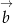 po obu stronach równości i mamy
po obu stronach równości i mamy
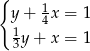
Odejmujemy od pierwszego równania drugie pomnożone przez 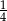 (żeby skrócić
(żeby skrócić  ).
).
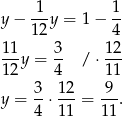
Stąd
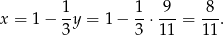
Teraz patrzymy na trójkąty  i
i 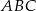 – trójkąty te mają wspólną podstawę, a stosunek ich wysokości jest równy
– trójkąty te mają wspólną podstawę, a stosunek ich wysokości jest równy
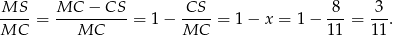
W takim razie
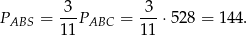
Analogicznie, patrząc na trójkąty 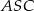 i
i 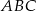 mamy
mamy
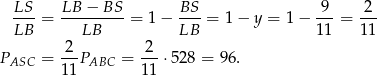
Teraz patrzymy na pary trójkątów 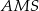 i
i 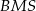 oraz
oraz 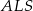 i
i 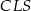 – stosunek pól tych trójkątów jest równy stosunkowi ich podstaw, więc
– stosunek pól tych trójkątów jest równy stosunkowi ich podstaw, więc
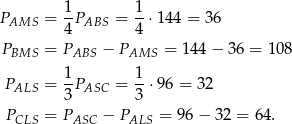
Odpowiedź: