Zadanie nr 6713579
Wyraź pole trójkąta w zależności od długości jednego z jego boków i miar kątów doń przyległych.
Rozwiązanie
Wyznaczymy pole trójkąta 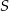 w zależności od boku
w zależności od boku  i przyległych kątów
i przyległych kątów 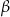 i
i 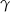 .
.
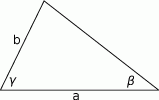
Punktem wyjścia jest znany wzór
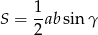
który łatwo wynika z twierdzenia sinusów. Wystarczy teraz wyliczyć  . Aby to zrobić stosujemy twierdzenie sinusów
. Aby to zrobić stosujemy twierdzenie sinusów
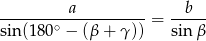
czyli
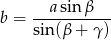
Otrzymujemy stąd wzór na pole
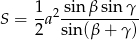
Odpowiedź: