/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Pole

Zadanie nr 6785158

Dodaj do ulubionych
Dodaj do rozwiązanych

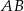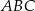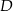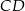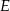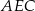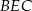Na boku AB trójkąta ABC wybrano punkt D , a na odcinku CD wybrano punkt E . Wykaż, że stosunek pól trójkątów AEC i BEC jest równy stosunkowi pól trójkątów 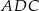ADC i BDC .

PIC

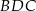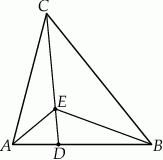
Rozwiązanie

Sposób I

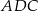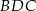Zauważmy najpierw, że trójkąty ADC i BDC mają wspólną wysokość opuszczoną z wierzchołka C .

PIC

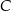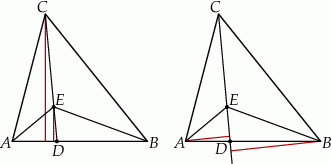
Stosunek ich pól jest więc równy stosunkowi ich podstaw:

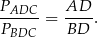
PADC-- AD-- P = BD . BDC

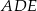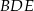Dokładnie tak samo jest w przypadku trójkątów ADE i BDE (trójkąty te mają wspólną wysokość opuszczoną z wierzchołka 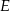E ). Zatem

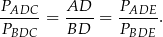
PADC AD PADE ------= ----= ------. PBDC BD PBDE

Pozostało zatem wykazać, że

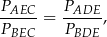
PAEC PADE ------= ------, PBEC PBDE

czyli równoważnie

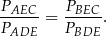
PAEC PBEC ------= -----. PADE PBDE

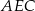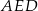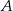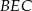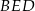To jednak uzasadniamy dokładnie tak samo jak poprzednio: trójkąty AEC i AED mają wspólną wysokość opuszczoną z wierzchołka A , a trójkąty BEC i BED mają wspólną wysokość opuszczoną z wierzchołka 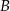B . Zatem

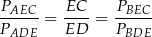
-PAEC- -EC- -PBEC- PADE = ED = PBDE

Sposób II

Tak jak poprzednio zauważamy, że

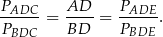
PADC--= AD--= PADE--. PBDC BD PBDE

Teraz skorzystamy z użytecznej obserwacji:

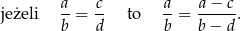
jeżeli a-= -c to a-= a−--c. b d b b− d

(Sprawdźcie, że tak jest!) Mamy zatem

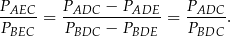
P P − P P -AEC--= -ADC-----ADE--= -ADC-. PBEC PBDC − PBDE PBDC

Sposób III

Oznaczmy 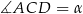∡ACD = α i ∡BCD = β .

PIC

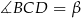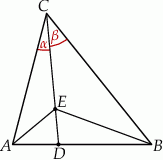
Ze wzoru na pole trójkąta z sinusem, mamy

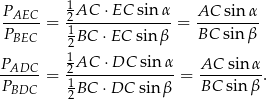
PAEC 12AC ⋅EC sin α AC sin α ------= 1--------------= --------- PBEC 2BC ⋅EC sin β BC sin β P 1AC ⋅DC sinα AC sinα -ADC--= 21--------------= ---------. PBDC 2BC ⋅DC sin β BC sin β

Zatem rzeczywiście

P P -AEC--= --ADC-. PBEC PBDC
Wersja PDF