/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Pole

Zadanie nr 9211229

Dodaj do ulubionych
Dodaj do rozwiązanych

Miary kątów trójkąta są w stosunku 1:2:3. Obwód koła opisanego na tym trójkącie jest równy 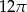1 2π . Oblicz pole tego trójkąta.

Rozwiązanie

Najpierw zastanówmy się ile wynoszą kąty w tym trójkącie. Oznaczmy przez α najmniejszy kąt w trójkącie. Wiemy, że pozostałe są odpowiednio dwa i trzy razy większe. Stąd otrzymujemy równanie

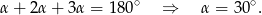
α + 2α + 3α = 180∘ ⇒ α = 30∘.

Mamy zatem do czynienia z trójkątem prostokątnym o kątach 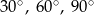30∘, 60∘, 9 0∘ . Teraz możemy wykonać rysunek.

PIC

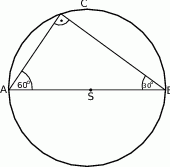
Bok 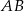AB jest średnicą okręgu, więc ze wzoru na obwód możemy wyznaczyć jego długość

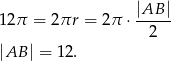
|AB-| 12π = 2πr = 2π ⋅ 2 |AB | = 12.

Wyznaczamy długość boku 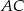AC

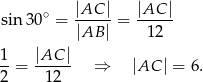
|AC | |AC | sin 30∘ = ----- = ----- |AB | 12 1- |AC-| 2 = 12 ⇒ |AC | = 6.

Obliczamy długość boku 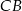CB

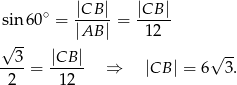
∘ |CB-| |CB-|- sin6 0 = |AB | = 12 √ -- --3-= |CB--| ⇒ |CB | = 6√ 3. 2 12

Zatem pole wynosi

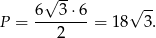
√ -- √ -- P = 6--3-⋅6-= 18 3. 2

 
Odpowiedź: √ -- 18 3

Wersja PDF