/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Pole

Zadanie nr 9328270

Dodaj do ulubionych
Dodaj do rozwiązanych

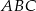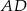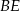W trójkącie ABC poprowadzono wysokości AD i BE oraz dwusieczną 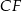CF . Wiedząc, że 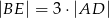|BE | = 3⋅ |AD | oblicz stosunek pól trójkątów 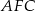AF C i BCF .

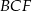Rozwiązanie

Rozpoczynamy od rysunku.

PIC

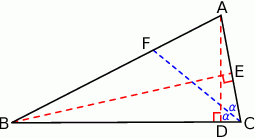
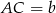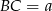Jeżeli AC = b oraz BC = a to ze wzoru na pole trójkąta mamy

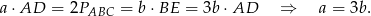
a⋅AD = 2PABC = b⋅BE = 3b ⋅AD ⇒ a = 3b.

Sposób I

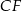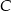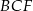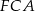Ponieważ prosta CF jest dwusieczną kąta C , kąty BCF i FCA są równe, oznaczmy tę wspólną miarę przez α . Ze wzoru na pole trójkąta z sinusem, mamy

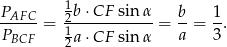
1 PAFC-= 2-b⋅CF--sin-α-= b-= 1. PBCF 12 a⋅CF sin α a 3

Sposób II

Na mocy twierdzenia o dwusiecznej mamy

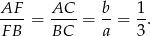
AF AC b 1 ----= ----= --= --. FB BC a 3

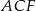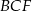Tyle samo jest równy interesujący nas stosunek pól, bo trójkąty ACF i BCF mają wspólną wysokość opuszczoną z wierzchołka C .  
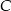Odpowiedź: 13

Wersja PDF