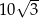/Szkoła średnia/Geometria/Planimetria/Trójkąt/Dowolny/Pole

Zadanie nr 9643596

W trójkącie 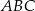ABC dane są: 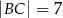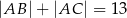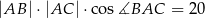|BC | = 7 , |AB |+ |AC | = 13 , |AB |⋅|AC |⋅co s∡BAC = 20 . Oblicz pole tego trójkąta.

Wersja PDF

Rozwiązanie

Oznaczmy 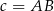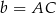c = AB , b = AC i α = ∡A .

PIC

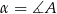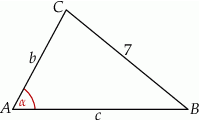
Przy tych oznaczeniach podane informacje możemy zapisać w postaci

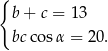
{ b + c = 13 bcco sα = 2 0.

Aby pozbyć się w tym układzie 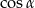cosα piszemy twierdzenie cosinusów.

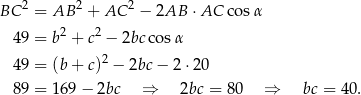
2 2 2 BC = AB + AC − 2AB ⋅ AC co sα 49 = b2 + c2 − 2bcc osα 2 49 = (b + c) − 2bc − 2 ⋅20 89 = 16 9− 2bc ⇒ 2bc = 80 ⇒ bc = 40.

Otrzymujemy stąd

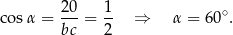
20- 1- ∘ cos α = bc = 2 ⇒ α = 60 .

Ponadto liczby 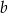b i c spełniają układ równań

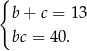
{ b + c = 13 bc = 40.

Na mocy wzorów Viète’a liczby te są rozwiązaniem równania

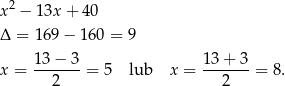
x 2 − 13x + 40 Δ = 169 − 16 0 = 9 x = 13-−-3-= 5 lub x = 13-+-3-= 8. 2 2

Mamy stąd 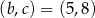(b,c) = (5,8) lub odwrotnie. W obu przypadkach pole trójkąta 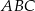ABC jest równe

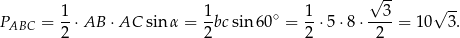
√ -- 1- 1- ∘ 1- --3- √ -- PABC = 2 ⋅AB ⋅ AC sin α = 2 bcsin 60 = 2 ⋅5 ⋅8 ⋅ 2 = 10 3.

 
Odpowiedź: √ -- 10 3

Wersja PDF