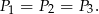Zadanie nr 9932598
Udowodnij, że trzy środkowe rozcinają trójkąt na sześć części o równych polach.
Rozwiązanie
Rozpoczynamy od szkicowego rysunku.
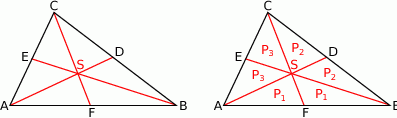
Sposób I
Zauważmy, że trójkąty 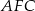 i
i 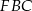 mają wspólną wysokość z trójkątem
mają wspólną wysokość z trójkątem 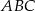 (opuszczoną z wierzchołka
(opuszczoną z wierzchołka 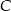 ). Ponadto, podstawy w tych trójkątach, na które jest opuszczona ta wysokość są dwa razy krótsze, niż podstawa trójkąta
). Ponadto, podstawy w tych trójkątach, na które jest opuszczona ta wysokość są dwa razy krótsze, niż podstawa trójkąta 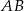 . To oznacza, że
. To oznacza, że
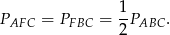
Wiemy ponadto, że punkt przecięcia środkowych dzieli każdą z nich w stosunku 2:1 (licząc od wierzchołka). To oznacza, że
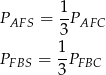
(trójkąty te mają wspólną wysokość opuszczoną na prostą 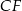 , oraz
, oraz 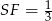 CF). Stąd
CF). Stąd
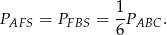
Analogicznie uzasadniamy, że
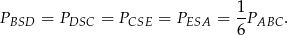
Sposób II
Tym razem postaramy się nie korzystać z twierdzenia o stosunku podziału środkowych (tak naprawdę po drodze udowodnimy to twierdzenie).
Zauważmy, że mamy 3 pary trójkątów o równych polach
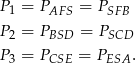
Tak jest, bo trójkąty każdej z tych par mają podstawy równej długości i wspólne wysokości opuszczone na te podstawy, np. dla trójkątów 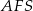 i
i 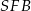 są to podstawy
są to podstawy 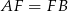 i wysokość opuszczona z wierzchołka
i wysokość opuszczona z wierzchołka 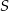 .
.
Zauważmy ponadto, że
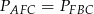
(trójkąty mają równe podstawy 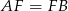 i wspólną wysokość opuszczoną z wierzchołka
i wspólną wysokość opuszczoną z wierzchołka 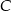 ). Mamy stąd
). Mamy stąd
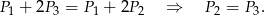
Podobnie, z równości
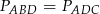
otrzymujemy
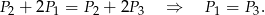
Udowodniliśmy więc, że