Zadanie nr 3906229
Dana jest funkcja 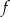 określona wzorem
określona wzorem 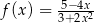 dla każdej liczby rzeczywistej
dla każdej liczby rzeczywistej  , oraz dwie liczby:
, oraz dwie liczby: 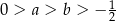 . Oblicz wartość wyrażenia
. Oblicz wartość wyrażenia
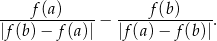
Rozwiązanie
Dane wyrażenie możemy zapisać w postaci
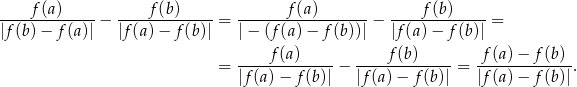
Zanim przekształcimy to wyrażenie dalej, musimy ustalić jaki jest znak liczby 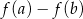 . W tym celu liczymy pochodną funkcji
. W tym celu liczymy pochodną funkcji 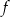 .
.
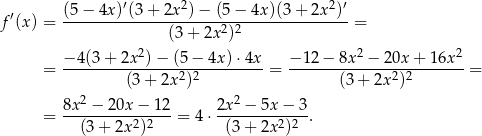
Rozkładamy jeszcze trójmian w liczniku otrzymanego ułamka.
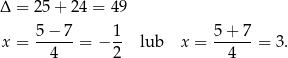
Mamy zatem
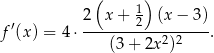
W szczególności, pochodna funkcji 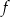 jest ujemna w przedziale
jest ujemna w przedziale 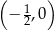 , czyli funkcja
, czyli funkcja 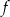 jest malejąca w tym przedziale. To oznacza, że
jest malejąca w tym przedziale. To oznacza, że 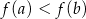 (bo
(bo 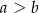 z założenia) oraz dane wyrażenie jest równe
z założenia) oraz dane wyrażenie jest równe
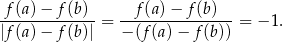
Odpowiedź: