/Szkoła średnia/Funkcje/Wymierna

Zadanie nr 6362203

Dodaj do ulubionych
Dodaj do rozwiązanych

Maksymalny zbiór, na którym funkcja rzeczywista

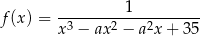
1 f(x ) = -3-----2----2------- x − ax − a x + 35

jest rosnąca jest jedyny i jest niepustym przedziałem postaci 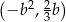( 2 2 ) −b ,3 b , dla pewnej liczby całkowitej 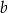b . Wyznacz dziedzinę funkcji 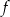f oraz jej największą wartość na przedziale [− 2,3] .

Rozwiązanie

Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Zaloguj się Informacje o abonamencie
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.