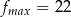/Szkoła średnia/Funkcje/Wymierna

Zadanie nr 6775083

Dodaj do ulubionych
Dodaj do rozwiązanych

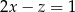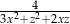Liczby rzeczywiste x i z spełniają warunek 2x − z = 1 . Wyznacz takie wartości x i z , dla których wyrażenie 3x2+z42+-2xz- przyjmuje największą wartość. Podaj tę największą wartość.

Rozwiązanie

Zauważmy najpierw, że ułamek ma tym większą wartość, im mniejszy jest jego mianownik. Z tego powodu zajmiemy się znalezieniem najmniejszej możliwej wartości funkcji kwadratowej w mianowniku danego wyrażenia.

Wiemy, że 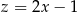z = 2x − 1 , więc interesuje nas wartość wyrażenia

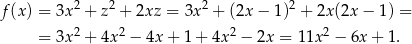
f(x) = 3x 2 + z2 + 2xz = 3x2 + (2x − 1)2 + 2x (2x − 1) = 2 2 2 2 = 3x + 4x − 4x+ 1+ 4x − 2x = 1 1x − 6x + 1.

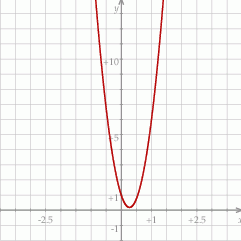
Wykresem tej funkcji jest parabola o ramionach skierowanych w górę i wierzchołku w punkcie

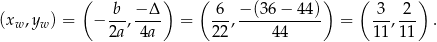
( ) ( ) ( ) b-- −Δ-- -6- −-(36-−-44)- -3- -2- (xw,yw ) = − 2a, 4a = 22 , 4 4 = 11 ,11 .

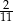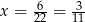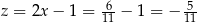W takim razie najmniejsza możliwa wartość tej funkcji kwadratowej to 121 i otrzymamy ją dla x = 262 = 311- i z = 2x − 1 = 611-− 1 = − 511 .

PIC

Dla tych samych wartości otrzymujemy największą możliwą wartość wyrażenia

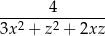
------4-------- 3x2 + z2 + 2xz

i jest ona równa

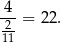
4--= 2 2. 121

 
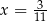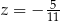Odpowiedź: 3- x = 11 , -5 z = − 11 , fmax = 22

Wersja PDF