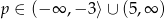/Szkoła średnia/Funkcje/Wymierna

Zadanie nr 7911224

Dodaj do ulubionych
Dodaj do rozwiązanych

Wyznacz te wartości parametru 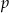p , dla których dziedziną funkcji 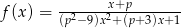f (x) = (p2−9)xx2++p(p+3)x+1 jest zbiór liczb rzeczywistych.

Rozwiązanie

To co mamy sprawdzić, to dla jakich wartości 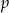p mianownik nie ma miejsc zerowych.

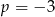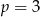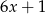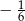Sprawdźmy najpierw co się dzieje jeżeli mianownik jest liniowy. Jeżeli p = − 3 to mamy w mianowniku 1 i jest OK. Jeżeli p = 3 , to mamy 6x + 1 i 1 − 6 nie należy do dziedziny danej funkcji.

Jeżeli 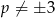p ⁄= ± 3 to mamy w mianowniku funkcję kwadratową i aby nie miała ona pierwiastków musimy mieć Δ < 0 .

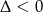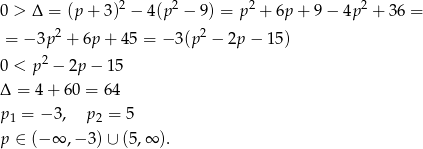
2 2 2 2 0 > Δ = (p + 3) − 4(p − 9) = p + 6p + 9 − 4p + 36 = = − 3p 2 + 6p + 45 = − 3(p2 − 2p − 1 5) 0 < p 2 − 2p − 15 Δ = 4+ 60 = 64 p1 = − 3 , p2 = 5 p ∈ (− ∞ ,− 3) ∪ (5,∞ ).

 
Odpowiedź: p ∈ (− ∞ ,− 3⟩ ∪ (5,∞ )

Wersja PDF