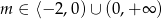Zadanie nr 9665840
Dla jakich wartości parametru 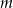 dziedziną funkcji
dziedziną funkcji 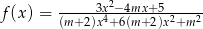 jest zbiór liczb rzeczywistych?
jest zbiór liczb rzeczywistych?
Rozwiązanie
Musimy sprawdzić dla jakich 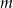 mianownik nie ma miejsc zerowych. Jeżeli
mianownik nie ma miejsc zerowych. Jeżeli 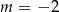 , to w mianowniku mamy 4 i jest OK. Jeżeli
, to w mianowniku mamy 4 i jest OK. Jeżeli 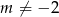 to mamy w mianowniku funkcję dwukwadratową. Podstawiając
to mamy w mianowniku funkcję dwukwadratową. Podstawiając 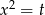 mamy trójmian
mamy trójmian
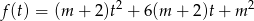
i musimy sprawdzić kiedy 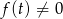 dla
dla 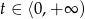 (bo takie wartości przyjmuje
(bo takie wartości przyjmuje 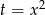 ).
).
Zauważmy, że 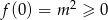 , zatem gdyby współczynnik przy
, zatem gdyby współczynnik przy 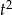 był ujemny, to funkcja
był ujemny, to funkcja 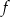 musiałaby mieć nieujemny pierwiastek i byłoby źle. Zatem musi być
musiałaby mieć nieujemny pierwiastek i byłoby źle. Zatem musi być
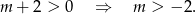
Zauważmy ponadto, że wierzchołek paraboli ma pierwszą współrzędną równą
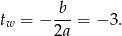
W połączeniu z warunkiem 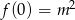 oznacza to, że
oznacza to, że 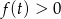 dla
dla 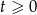 o ile tylko
o ile tylko 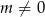 (funkcja rośnie na prawo od -3, jeżeli więc
(funkcja rośnie na prawo od -3, jeżeli więc 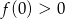 , to taka sama nierówność jest prawdziwa dla wszystkich liczb dodatnich).
, to taka sama nierówność jest prawdziwa dla wszystkich liczb dodatnich).
Odpowiedź: