/Szkoła średnia/Geometria/Planimetria/Czworokąt/Dowolny/Kąty

Zadanie nr 1343415

Dodaj do ulubionych
Dodaj do rozwiązanych

Wszystkie wierzchołki czworokąta 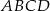ABCD leżą na okręgu oraz 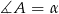∡A = α . Oblicz miarę kąta ∡C .

PIC

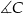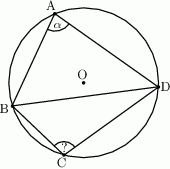
Rozwiązanie

Dorysujmy promienie 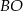BO i DO .

PIC

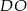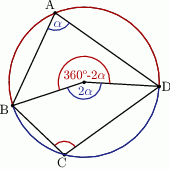
Kąt środkowy 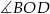∡BOD oparty na łuku 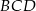BCD jest dwa razy większy od kąta wpisanego 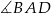∡BAD opartego na tym samym łuku, ma więc on miarę 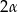2α . To oznacza, że drugi z kątów środkowych 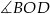∡BOD (ten oparty na łuku 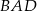BAD ) ma miarę 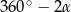∘ 360 − 2α . Teraz ponownie korzystamy z zależności między kątami: wpisanym i środkowym.

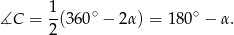
1 ∡C = -(360∘ − 2α ) = 180∘ − α. 2

 
Odpowiedź: ∘ 180 − α

Wersja PDF