Zadania.info
Największy internetowy zbiór zadań z matematyki
cornersUpL
cornersUpR

Zadania

Na skróty

Recenzje

Linki sponsorowane

cornersM
Zaloguj się

Linki sponsorowane

cornersR
Zadanie nr 2883750

W czworokącie wypukłym 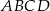ABCD dane są długości jego boków i miara kąta 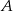A . Wyznacz miary pozostałych kątów tego czworokąta.

Wersja PDF
Rozwiązanie

Przyjmijmy oznaczenia jak na rysunku.

PIC

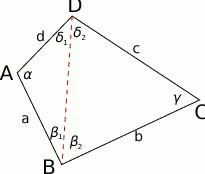
Pierwsza obserwacja, to że korzystając z twierdzenia cosinusów, możemy łatwo wyliczyć długość przekątnej 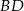BD

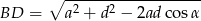
∘ ------------------- BD = a2 + d2 − 2ad cosα

Ponieważ ta długość przekątnej będzie wielokrotnie występować w dalszych rachunkach, oznaczmy ją przez e . Będziemy pamiętać, że mamy to wyliczone.

Stosując ponownie twiedzenie cosinusów, ale tym razem w trójkącie 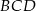BCD otrzymujmy

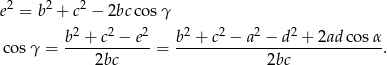
2 2 2 e = b + c − 2bc cosγ b2 + c2 − e2 b2 + c2 − a2 − d2 + 2ad cosα cos γ = ------------ = ----------------------------. 2bc 2bc

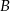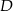Przyjemną część zadania mamy za sobą, zostało teraz wylicznie kątów B i D . Zrobimy to rozbijając je na dwa kąty (jak na rysunku) i korzystając ze wzoru

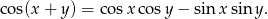
cos(x + y) = co sx cosy − sin xsiny .

Z twierdzenia sinusów w trójkącie 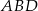ABD

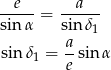
--e-- --a--- sin α = sin δ a 1 sin δ1 = --sinα e

Podobnie z trójkąta 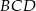BCD mamy

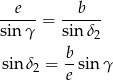
e b ----- = ------ sin γ sin δ2 b- sin δ2 = e sinγ

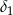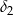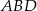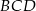Potrzebujemy jeszcze cosinusy kątów δ1 i δ2 . Wyliczamy je z twierdzenia cosinusów w trójkątch ABD i BCD odpowiednio.

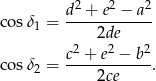
d2 + e2 − a2 cosδ1 = ------------ 2 2d2e 2 cosδ = c-+-e--−-b-. 2 2ce

Możemy w końcu wyliczyć 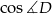cos∡D :

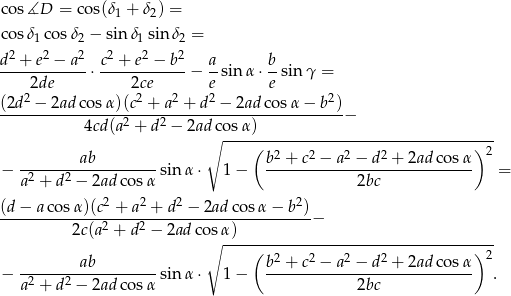
co s∡D = cos(δ + δ ) = 1 2 co sδ1cos δ2 − sin δ1sin δ2 = d2 + e2 − a2 c2 + e2 − b2 a b ------------⋅ ------------− -sin α⋅ --sin γ = 2de 2ce e e (2d2-−-2ad-cos-α)(c2 +-a2 +-d-2 −-2ad-cos-α-−-b2) 4cd(a2 + d2 − 2ad cosα) − ∘ ------------------------------------- ab (b 2 + c2 − a2 − d2 + 2ad cosα ) 2 − -2----2------------sinα ⋅ 1− ----------------------------- = a + d − 2ad cosα 2bc (d − a cosα)(c2 + a2 + d2 − 2ad cosα − b 2) --------------2----2-----------------------− 2c(a + d − 2ad co∘sα-)----------------------------------- ( 2 2 2 2 ) 2 − --------ab---------sinα ⋅ 1− b--+-c--−-a--−-d--+-2ad-cosα- . a2 + d2 − 2ad cosα 2bc

Analogicznie wyliczamy 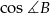cos∡B .

Wersja PDF
Twoje uwagi
Nie rozumiesz fragmentu rozwiązania?
W rozwiązaniu jest błąd lub literówka?
Masz inny pomysł na rozwiązanie tego zadania?
Napisz nam o tym!