/Konkursy/Zadania/Liczby/Ułamki

Zadanie nr 6759922

Pewnego dnia postawiłem dla psów miskę z psimi ciasteczkami. Najpierw przyszedł najstarszy pies i zjadł połowę ciasteczek, i jeszcze jedno. Potem przyszedł drugi pies zjadł połowę tego, co znalazł i jeszcze jedno ciasteczko. Potem przyszedł trzeci pies i także zjadł połowę tego, co znalazł i jeszcze jedno ciasteczko. Wreszcie przyszedł czwarty najmniejszy piesek i zjadł połowę tego, co zostało, i jeszcze jedno ciasteczko, wtedy ciasteczka się skończyły. Ile ich było na początku w misce?

Wersja PDF

Rozwiązanie

Sposób I

Niech x liczba ciasteczek.
Pierwszy pies zjadł 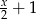x+ 1 2 ciastek, zostało x − 1 2 .
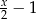Drugi pies zjadł

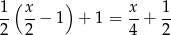
1 ( x ) x 1 2- 2-− 1 + 1 = 4-+ 2-

Zostało

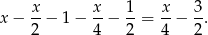
x- x- 1- x- 3- x− 2 − 1 − 4 − 2 = 4 − 2 .

Trzeci pies zjadł

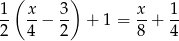
( ) 1- x− 3- + 1 = x-+ 1- 2 4 2 8 4

Zostało

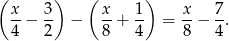
( ) ( ) x- 3- x- 1- x- 7- 4 − 2 − 8 + 4 = 8 − 4.

Ostatni pies zjadł

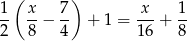
( ) 1 x 7 x 1 -- --− -- + 1 = ---+ -- 2 8 4 16 8

Zostało

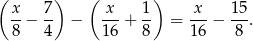
( x 7) ( x 1 ) x 1 5 --− -- − ---+ -- = ---− ---. 8 4 16 8 16 8

Ponieważ wiemy, że na koniec nie zostały żadne ciastka, to mamy równanie

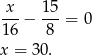
x--− 1-5 = 0 16 8 x = 30.

Sposób II

Tym razem liczymy ciasteczka od końca.

Wiemy, że gdy ostatni piesek zjadł połowę pozostałych ciasteczek to zostało jedno ciastko (bo jak je zjadł, to ciastka się skończyły). Zatem czwarty piesek zastał 2 ciasteczka. To oznacza, że trzeci piesek zastał

2⋅ (2+ 1) = 6

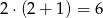
ciastek (bo jak zjadł połowę i jeszcze jedno to zostały 2). Zatem drugi zastał

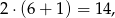
2 ⋅(6+ 1) = 14,

a pierwszy

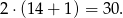
2 ⋅(14 + 1) = 30.

Sposób III

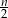Powyższe rozumowanie można zgrabnie zapisać używając dwójkowego systemu pozycyjnego. Z informacji o pierwszym piesku wynika, że liczba ciastek n jest parzysta, czyli ostatnią cyfrą w zapisie dwójkowym liczby ciastek jest 0. Z informacji o drugim piesku wynika, że liczba n 2 jest nieparzysta, co oznacza, że druga (od prawej) cyfra zapisu n w systemie dwójkowym jest równa 1. Podobnie ustalamy, że kolejne trzy cyfry są równe 1. Zatem

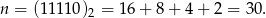
n = (11 110)2 = 16 + 8 + 4 + 2 = 30 .

 
Odpowiedź: 30

Wersja PDF