Zadanie nr 2179190
Wszystkie potęgi liczby 3 oraz wszystkie te dodatnie liczby naturalne, które są skończonymi sumami różnych potęg liczby 3, ustawiamy w ciąg rosnący 1,3,4,9,10,12,13,…Ile jest równy setny wyraz tego ciągu?
A) 150 B) 981 C) 1234 D) 2401 E)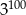 
Rozwiązanie
Liczby, o których mowa w zadaniu, to liczby, których zapis w systemie trójkowym składa się z samych 1 i 0.
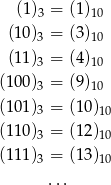
Sposób I
Łatwo zauważyć, że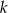 
-cyfrowych takich liczb jest 
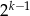– bo liczb 
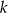cyfrowych jest dokładnie tyle ile wszystkich liczb o ilości cyfr mniejszej od 
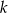(0 traktujemy jako 0-cyfrowe), stąd łatwo indukcyjnie wyznaczyć ich ilość.
Ponieważ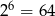 
, więc pierwsze 63 liczby w naszym ciągu (64 razem z 0!), to liczby o mniej niż 7 cyfrach. 64 liczba to pierwsza liczba 7 cyfrowa 
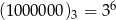. Możemy zatem zapomnieć o pierwszej cyfrze i sprowadzamy zadanie do prostszego, musimy ustalić jak wygląda 
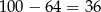liczba w tym ciągu. Robimy to jak poprzednio, 
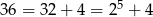, jest to więc 5 liczba 6-cyfrowa, czyli 
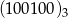. Szukana liczba to zatem
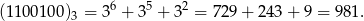
Sposób II
Zauważmy, że liczby wypisane w lewej kolumnie, to dokładnie kolejne liczby naturalne zapisane w systemie o podstawie 2. Zatem setną będzie 100 rozpisane przy podstawie 2, czyli
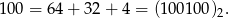
Jako liczba przy podstawie 3, będzie ona równa
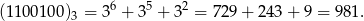
Odpowiedź: B
