Zadanie nr 4257074
Na kartce napisano w jednej linii kilka różnych liczb całkowitych dodatnich nie większych niż 10. Oglądając tę kartkę, Mirek stwierdził ze zdumieniem, że w każdej parze sąsiednich liczb jedna z nich dzieli drugą. Ile co najwyżej liczb mogło byc napisanych na tej kartce?
A) 6 B) 7 C) 8 D) 9 E) 10
Rozwiązanie
Chwilę kombinując, można znaleźć ciąg długości 9
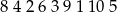
spróbujmy uzasadnić, że nie ma ciągu długości 10. W takim ciągu musi być 7 i musi być ona na końcu lub początku, sąsiadując z 1. Są jeszcze dwie liczby, które muszą być z brzegu lub obok 1: 5 i 9.
Powiedzmy, że 5 jest obok 1. Mamy wtedy ciąg
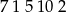
i zostały nam jeszcze 3,4,6,8,9. Jeżeli teraz napiszemy 4 lub 8, to nie uda nam się już dopisać żadnej liczby podzielnej przez 3. Jeżeli natomiast napiszemy 6, to nie uda nam się dopisać ani 4 ani 8.
Druga możliwość to początek typu
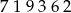
Teraz mamy trzy możliwe zakończenia:
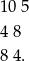
W każdej sytuacji mamy ciąg krótszy niż 9.
Odpowiedź: D

