Zadanie nr 6080014
Liczbę pierwszą nazywamy specjalną jeżeli jest jednocyfrową liczbą pierwszą albo liczbą pierwszą o większej liczbie cyfr, ale taką, że po skreśleniu dowolnej skrajnej cyfry zawsze otrzymamy specjalną liczbę pierwszą. Ile jest specjalnych liczb pierwszych?
A) 4 B) 7 C) 8 D) 9 E) 11
Rozwiązanie
Cała trudność w zadaniu polega na uważnym wypisaniu tych liczb.
Liczby jednocyfrowe to 2,3,5,7.
Liczby dwucyfrowe muszą składać się z powyższych cyfr i nie mogą mieć na końcu ani 2 ani 5 (bo mają być pierwsze). Od razu wypisujemy tylko te, które są pierwsze.
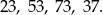
Teraz liczby trzycyfrowe. Zarówno pierwsze dwie, jak i ostatnie dwie cyfry takiej liczby muszą jedną z 4 wypisanych wyżej specjalnych liczb dwucyfrowych. Daje nam to możliwości
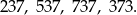
Pierwsze dwie dzielą się przez 3, a trzecia dzieli się przez 11. Zostaje tylko 373.
To oznacza, że nie ma czterocyfrowych specjalnych liczb pierwszych, bo taka liczba musiałaby się zaczynać od 373 i tak samo kończyć. Zatem wypisaliśmy wszystkie specjalne liczby pierwsze.
Odpowiedź: D

