Zadanie nr 7915717
Rysunek obok przedstawia kwadratową płytkę. Narysowane na niej linie krzywe są ćwiartkami okręgów o promieniu równym połowie boku płytki. Długość takiej ćwiartki jest równa 5 dm. Z szesnastu takich płytek budujemy kwadrat. Jaką maksymalną długość może mieć nieprzerwana linia utworzona z ćwiartek tych okręgów?

A) 75 dm B) 100 dm C) 105 dm D) 110 dm E) 80 dm
Rozwiązanie
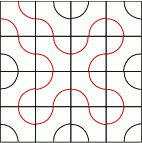
Jedyny sposób na rozwiązanie tego zadania to porobić sobie kilka takich dużych kwadratów i próbować rysować długie krzywe. W pierwszej chwili może się wydawać, że najdłuższa krzywa jest taka jak na pierwszym rysunku.
Zacznijmy się zastanawiać nad uzasadnieniem. W wewnętrznych 4 płytkach nasza krzywa przechodzi przez obydwa łuki i to dobrze. Na brzegach nie może przechodzić przez obydwa łuki, chyba że akurat w tej płytce się kończy. No właśnie, końce są dwa, czyli dwie płytki brzegowe mogą być wypełnione maksymalnie, a na pierwszym rysunku wypełniona jest tylko jedna. Wystarczy jednak mała modyfikacja i już mamy maksymalną krzywą – rysunek drugi. Składa się on z 22 pojedynczych łuków, czyli ma długość 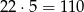 .
.
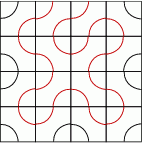
Odpowiedź: D

