Zadanie nr 9308146
Niech 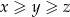 będą dodatnimi liczbami rzeczywistymi takimi, że
będą dodatnimi liczbami rzeczywistymi takimi, że 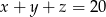 . Które z poniższych zdań jest prawdziwe?
. Które z poniższych zdań jest prawdziwe?
A) Zawsze 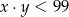
B) Zawsze 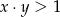
C) Zawsze 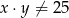
D) Zawsze 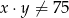
E) Żadne z poprzednich zdań nie jest prawdziwe.
Rozwiązanie
Zastanówmy się kolejno nad każdym z warunków.
A) Liczby  i
i 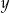 możemy wziąć dowolnie bliskie 10 i wtedy
możemy wziąć dowolnie bliskie 10 i wtedy 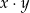 będzie dowolnie bliskie 100, np.
będzie dowolnie bliskie 100, np. 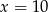 ,
, 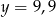 ,
, 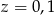 to
to 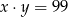 .
.
B) Jeżeli  weźmiemy bardzo bliskie 20, to
weźmiemy bardzo bliskie 20, to 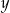 będzie dowolnie małe. Np.
będzie dowolnie małe. Np. 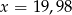 ,
, 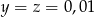 , to
, to 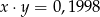 .
.
C) Łatwo znaleźć kontrprzykład, np. 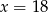 ,
, 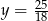 ,
, 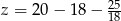 .
.
D) Jak poprzednio, np. 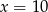 ,
, 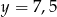 ,
, 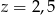 .
.
Odpowiedź: E

