/Konkursy/Zadania testowe

Zadanie nr 9737438

Dodaj do ulubionych
Dodaj do rozwiązanych

Kwadrat podzielono na 2009 kwadratów, których długości boków są liczbami całkowitymi. Jaką najmniejszą długość może mieć bok dzielonego kwadratu?
A) 44
B) 45
C) 46
D) 503
E) Nie można kwadratu podzielić na 2009 takich kwadratów.

Rozwiązanie

Pole każdego utworzonego kwadratu jest równe co najmniej 1, więc wyjściowy kwadrat musi mieć pole równe co najmniej 2009, czyli bok nie może być mniejszy niż

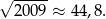
√ ----- 2009 ≈ 4 4,8.

Czyli najmniejszy możliwy bok to 45. Teraz pozostało sprawdzić, czy kwadrat boku 45 da się podzielić na 2009 kwadratów. Oczywiście można go podzielić na

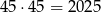
45 ⋅45 = 20 25

kwadratów. Ponieważ 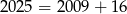2025 = 2009 + 16 musimy jakoś się pozbyć w tym rozkładzie 16 kwadracików. To jednak nie jest trudne bo jak zastąpimy dowolny kwadrat składający się 3x3=9 kwadratów jednym kwadratem, to zmniejszamy liczbę kwadratów o 8.

PIC

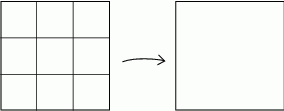
Wystarczy więc taką operację wykonać dwa razy.  
Odpowiedź: B

Wersja PDF