Zadanie nr 6514023
Jeżeli  i
i 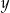 są liczbami całkowitymi o tej własności, że
są liczbami całkowitymi o tej własności, że 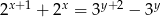 , to
, to  jest równe
jest równe
A) 0 B) 3 C) -1 D) 1 E) 2
Rozwiązanie
Przekształćmy podaną równość
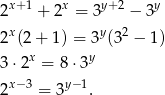
Widać stąd, że 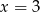 i
i 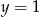 .
.
Odpowiedź: B
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Jeżeli  i
i 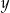 są liczbami całkowitymi o tej własności, że
są liczbami całkowitymi o tej własności, że 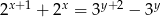 , to
, to  jest równe
jest równe
A) 0 B) 3 C) -1 D) 1 E) 2
Przekształćmy podaną równość
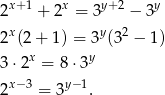
Widać stąd, że 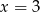 i
i 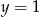 .
.
Odpowiedź: B
