Zadanie nr 6709593
Jaka jest najmniejsza liczba całkowita  , dla której liczba
, dla której liczba
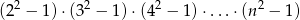
jest kwadratem liczby całkowitej?
A) 6 B) 8 C) 16 D) 27 E) Inna odpowiedź
Rozwiązanie
Przekształćmy podane wyrażenie
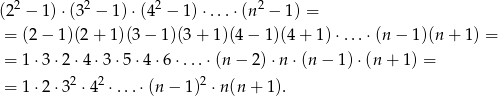
W przekształceniu skorzystaliśmy z tego, że oprócz pierwszych dwóch i ostatnich dwóch, każda liczba pojawia dokładnie w dwóch nawiasach. Widać zatem, że liczba ta będzie kwadratem jeżeli kwadratem będzie 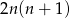 .
.
Można teraz po prostu sprawdzać kolejne wartości  , ale można też zauważyć, że bądź
, ale można też zauważyć, że bądź  , bądź
, bądź 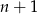 musi być kwadratem (bo
musi być kwadratem (bo  i
i 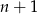 są względnie pierwsze i tylko jedna z nich może dzielić się przez 2). Sprawdzamy więc tylko
są względnie pierwsze i tylko jedna z nich może dzielić się przez 2). Sprawdzamy więc tylko 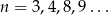 .
.
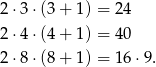
No i mamy kwadrat.
Odpowiedź: B

