Zadanie nr 7948791
Ile liczb sześciocyfrowych posiada tę własność, że każda ich cyfra, zaczynając od trzeciej, jest sumą dwóch poprzednich cyfr (cyfry liczymy od lewej strony)?
A) 1 B) 2 C) 3 D) 4 E) 6
Rozwiązanie
Jeżeli 
i 
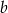to pierwsze dwie cyfry, to mamy kolejno
3 cyfra: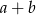 
4 cyfra: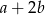 
5 cyfra: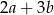 
6 cyfra: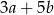 
Ostatnia cyfra musi być oczywiście nie większa niż 9, więc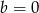 
lub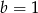 
. Jeżeli 
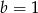to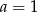 
i mamy liczbę
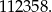
Jeśli natomiast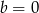 
, to 
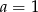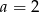lub 
lub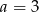 
. Mamy wtedy liczby
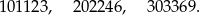
Odpowiedź: D
