Zadanie nr 3922482
Na powierzchni piłki namalowano trzy jednakowe okręgi, dzielące ją na osiem jednakowych części, jak na rysunku obok. Trzmiel, który usiadł na piłce w punkcie przecięcia okręgów, wędruje po namalowanych okręgach w taki sposób, że po przejściu ćwiartki okręgu w punkcie przecięcia z innym okręgiem zawsze skręca na przemian w w prawo albo w lewo, tj. w prawo, gdy w poprzedzającym punkcie skręcał w lewo, natomiast w lewo, gdy w poprzedzającym punkcie skręcał w prawo. Jaka jest najmniejsza liczba ćwiartek okręgów, które musi przejść trzmiel aby ponownie znalazł się w punkcie, z którego wyruszył?
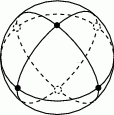
A) 6 B) 9 C) 12 D) 15 E) 18
Rozwiązanie
Startujemy z punktu 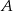 i jedziemy według opisanej procedury.
i jedziemy według opisanej procedury.
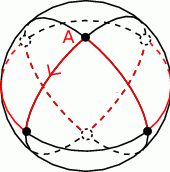
Widać, że do punktu wyjścia wracamy po 6 odcinkach.
Odpowiedź: A

